How To Obtain Sample Potential Data For Skpm Measurement
- 11 Oct 2017
- Volume 11
- NanoScientific Magazine, Fall 2017
INTRODUCTION
Scanning Kelvin probe microscopy, or SKPM, was introduced as a tool to measure the local contact potential difference between a conducting atomic force microscopy (AFM) tip and the sample, thereby mapping the work function or surface potential of the sample with high spatial resolution. Since its first introduction by Nonnenmacher [1], SKPM has been used extensively as a unique method to characterize the nanoscale electrical properties of metal or semiconductor surfaces and semiconductor devices. Recently, SKPM has also been used to study the electrical properties of organic materials, devices [2–4], and biological materials. To eliminate any confusion, let us look into SKPM’s synonyms for this technique:
· SKPM: Scanning Kelvin Probe Microscopy
· KPFM: Kelvin Probe Force Microscopy
· SSPM: Scanning Surface Potential Microscopy
· SKFM: Scanning Kelvin Force Microscopy
· SP-AFM: Surface Potential Atomic Force Microscope
MICROSCOPY
SKPM will be used in this document, as it is the most widely used descriptor for this technique. The term ’Kelvin force’ refers to similarities between this microscopic technique and the macroscopic technique, which is the Kelvin probe method. However, the methodology is somewhat different, but the measured value is equivalent for both techniques. For clarity, this note will refer only to the microscopic technique SKPM.
FUNDAMENTALS OF SKPM
The SKPM measures Contact Potential Difference (CPD) between a conducting AFM tip and a sample. The CPD (VCPD) between the tip and sample is defined as:
where sample and tip are the work functions of the sample and tip, and e is the electronic charge. The different Fermi energy levels between the AFM tip and sample surface causes an electrical force as the AFM tip is brought close to the sample surface. Figure1 shows the energy level diagram of the tip and sample surface when sample and tip are different. Figure1(a) depicts the energy levels of the tip and sample surface when separated tip and sample surface are close enough for electron tunneling, equilibrium of the states require Fermi levels to line-up at steady state. Upon electrical contact, the Fermi levels will align through electron current flow, and the system will reach to an equilibrium state as shown in Figure1(b). The tip and sample surface will be charged, and an apparent VCPD will be formed (note, the Fermi energy levels are aligned but the vacuum energy levels areno longer the same, and a VCPD between the tip and sample has been formed). An electrical force acts on the contact area, due to the VCPD. As shown in Figure1(c), this force can be nullified. This technique is the Kevin Probe method that relies on the detection of an electric field between a sample material and probe material. The electric field can be varied by the voltage VCPD, that is applied to the sample relative to the probe. If an applied external bias (VDC) has the same magnitude as the VCPD with opposite direction, the applied voltage eliminates the surface charge in the contact area.
The applied VCPD nullifies the electrical force and has the same value as the work function difference between the tip and the sample. This allows the work function of the sample to be calculated when the work function of the tip is known.
By applying an AC voltage (VAC) plus a DC voltage (VDC) to theAFM tip, SKPM measures the work function of the sample. VAC generates the oscillating electrical forces between the AFM tip andsample surface, and VDC nullifies the oscillating electrical forces that originated from CPD between the tip and the sample surface. The electrostatic force (Fes) between the AFM tip and sample is givenby:
(2.2) where z is the direction normal to the sample surface, ΔV is thepotential difference between VCPD and the voltage applied to the AFM tip, and dC/dz is the gradient of the capacitance between tipand sample surface. The external potential, VExt, is an additional voltage that is applied either to the tip or to the sample; the sign in front of VExt is explained below.The voltage difference ΔV will be [5]:
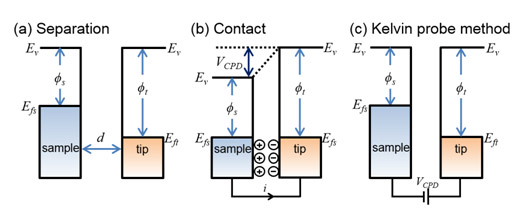
Figure 1. Electronic energy levels of the sample and AFM tip for three cases: (a) tip and sample are separated by distance d with no electrical contact, (b) tip and sample are in electrical contact, and (c) external bias (VDC) is applied between tip and sample to nullify the CPD and, therefore, the tip–sample electrical force. Ev is the vacuum energy level. Efs and Eft are Fermi energy levels of the sample and tip, respectively.
The amplitude of the tip vibration, Vac, is proportional tothe force F. Substituting the expression of the voltage given in Equations 2.2 and 2.3 and collecting the terms according to their frequencies, the following form for the amplitude of thetip vibration is obtained:
(2.4) This equation can be divided into three parts:
(2.5)(2.6)(2.7) FDC(Equation 2.5) results in a static deflection of the AFM tip. Fω with frequency ω (Equation2.6) is used to measure the VCPD, and F2ω is used for capacitance microscopy [6]. Fω is electrical force component modified with frequency ω It is also the function of VCPD and VAC. When electrostatic forces are applied to the tip by VAC with VExt, additional oscillating components (due to the electrical force) will be superimposed to the mechanical oscillation of the AFM tip. A lock-in amplifieris employed to measure the VCPD, to extract the Fω. The output signal of the lock-in amplifier is directly proportional to the difference between VCPD and VExt. The VCPD value can be measured by applying VExt to the AFM tip, such that the output signal of the lock-in amplifier is nullified and Fω reaches zero. Subsequently, the value of VExt is obtained for each point on the sample surface and maps the work function or surface potential of the whole sample surface area. The contact potential difference, VCPD, is obtained by the following procedure: the direct current VDC voltage, VExt, is varied until the alternating current VAC vibration of the tip at the frequency ω is nullified; at this voltage VExt=±VCPD.
When the external voltage is applied to the tip or to the sample it changes their work functions. Hence, based on Equation 2.1 the sign of VCPD will be different inthe two cases. The posteriori dc voltage difference (direction) VCPD is thus given for the two cases as:
(2.8)(2.9) where Equations 2.8 and 2.9 are for the cases of voltage applied to the sample and the tip, respectively. After the nullifying procedure, i.e., when VCPD, we obtain VExt=±VCPD, where the ‘+’ and ‘-’ refer to the external bias applied to the sample and the tip, respectively.
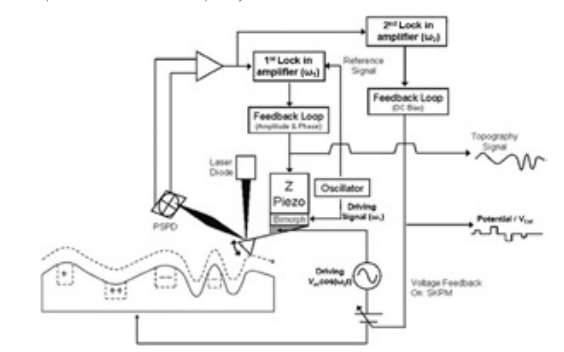
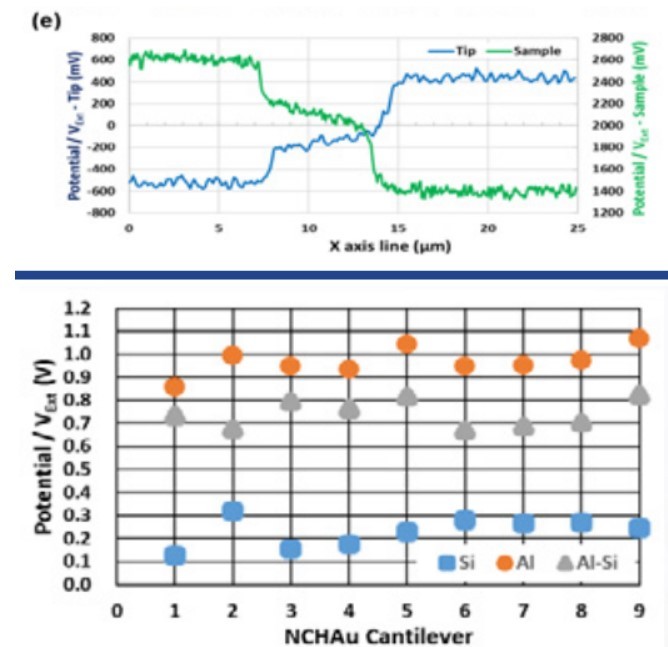
Figure 2. SKPM schematicused by Park Systems.Figure3 (e) is the line profile data of the mean values for 16 adjacent points along the y-axis. It can be seen in the metal regions in the potential difference(Vext) image that they are mutually inverted. This proves that the inverted signs, positive and negative expressions in Equations 2.8 and 2.9 are correct.
SKPM MODE FOR PARK SYSTEMS
There are various methods of measuring the SKPM mode in AFM. Among them, Park Systems uses two frequencies as showed in Figure 2. Two implemented lock-in amplifiers in the controller are used for each frequency moderation. One frequency is used to oscillate the cantilever and obtain a surface image using bimorph, which is the term for oscillating the cantilever using piezoelectric material. The other frequency directly signals the cantilever at 17.0 kHz, which is the frequency generally used for SKPM.
The topography signal and potential signal are acquired from each frequency simultaneously and two images are created without affecting each other. This allows the user to obtain a surface image and a potential image with a single scan. The topography signal is obtained by keeping the distance constant between the tip and sample, whereas the potential image is obtained by applying a default external voltage and potential measurement voltage on the cantilever as described in Figure 2. NCHAucantilever of NANOSENSORS was used for SKPM measurement. This model has a metallic layer coated on both sides of the cantilever and has a typical tip radius of curvature smaller than 50nm. The resonant frequency and force constant is 330 kHz and 42N/m, respectively. Here, the offset between the tip and the surface sample may occur as shown in Figure 3(e). The cause for this offset is the electrical factors that occurs from theVAC amplitude. Therefore, to know the offset in the SKPM measurement, it is necessary to measure the HOPG or a calibration sample, which havework function values that are known in advance. One point is to be noted—the difference between the Au and Al areas must be constant according to the applied direction because there is an absolute difference in work function.
ANALYSIS & REPEATABILITY ABOUT SKPM
The purpose of SKPM is to obtain the work function for the measuring specimen, not the VCPD between the tip and the sample. Therefore, accurate analysis is essential. To obtain the exact work function of the sample, it is necessary to measure several cantilevers and average them to obtain more accurate work function values of the samples.Calibration of the system must be done by using a sample that has a work function that is already known, for instance HOPG.First, a precise tip’s work function must be measured using the sample with a given work function. This process is done to eliminate the electrical offset that could possibly happen during SKPM measurement. Secondly, after measuring the SKPM of the sample, the work function of the tip is obtained by using Equation 2.10. Finally, repeating this process several times and averaging the results will produce more accurate results.
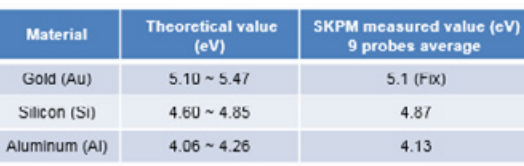
The sample consisted of three different materials: Au, Si, and Al. For the calibration surface sample, Au was selected to become the base material. The work function of Si and Al were determined as explained above. The theoretical work function values and the experimentally determined work function values of Si and Al are shown in Table 1.
Figure 3.25.0um x 12.5um SKPM images of the Au-Si-Al patterned sample. When applied to cantilever direction topography (a) and VExt(b). When applied to sample direction topography (c) and VExt(d). Scale bar is 5um. (e) is a VExt (potential difference) line profile according to the applied
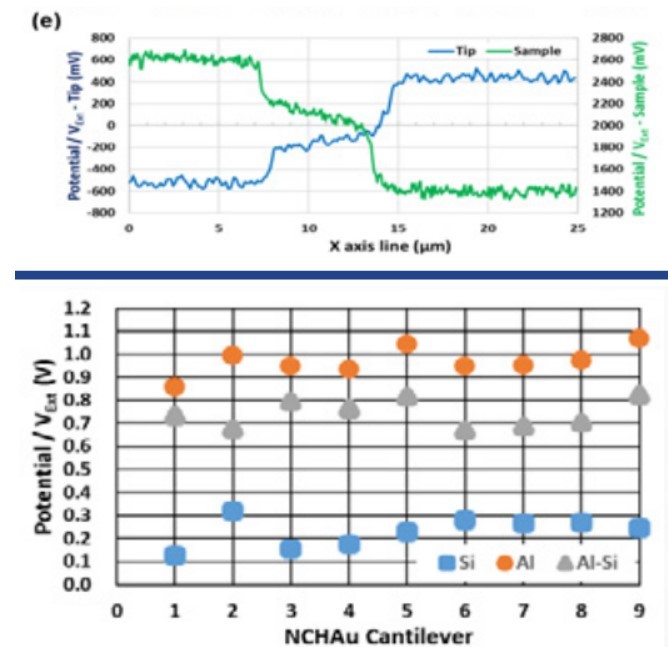
Figure 4. SKPM data obtained using nine different NCHAu (NANOSENSORS) probes on the Au-Si-Al patterned sample. The value on Al (orangecircles), Si (blue squares) and their differences (gray triangles) are plotted
Table1. Theoretical work function values and nine different NCHAu probes work function values for average for each of the three materials in the Au-Si-Al patterned sample. Park Systems offers a suite of SKPM measurement solutions that serve as a quantitative work function measurement
[1] M. Nonnenmacher, M.P. Oboyle, H.K. Wickramasinghe, Appl. Phys. Lett. 58(1991) 2921
[2] H. Hoppe, T. Glatzel, M. Niggemann, A. Hinsch, M.C. Lux-Steiner, N.S. Sariciftci,Nano Lett. 5 (2005) 269.
[3] T. Hallam, C.M. Duffy, T. Minakata, M. Ando, H. Sirringhaus, Nanotechnology 20 (2009) 025203.
[4] L.M. Liu, G.Y. Li, Appl. Phys. Lett. 96 (2010) 083302.
[5] R. Shikler, T. Meoded, N. Fried, B. Mishori, Y. Rosenwaks, J. Appl. Phys. 86 (1999) 107.
[6] S.V. Kalinin, A. Gruverman (Eds.), Scanning Probe Microscopy, Springer, New York, 2007.the base material. The work function of Si and Al were determined as explained above. The theoretical work function values and the experimentally determined work function values of Si and Al are shown in Table 1.